onlineoverland: Overland flow using the diffusion wave method --- One book
onlineoverland: Overland flow using the diffusion wave method --- One book
|
|
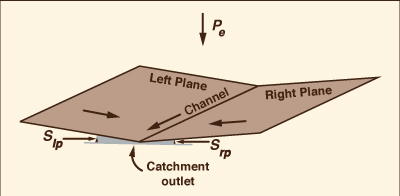
The simulation of catchment dynamics using a physically based overland flow model is well established in hydraulic and hydrologic engineering practice (Ponce 1986). The diffusion wave model is an improvement over the kinematic wave model because the former is grid independent, while the latter is not. In fact, it can be shown that the outflow hydrograph generated by the diffusion wave model does not vary with the choice of grid size, while the same statement does not hold true for the kinematic wave model. This correct numerical behavior is due to the fact that the diffusion wave model matches the physical diffusivity of Hayami with the numerical diffusivity of Cunge (Ponce 1989). In addition to matching diffusivities, ONLINE OVERLAND minimizes numerical dispersion by specifying the grid ratio such that the Courant number is equal to 1. This leads to a simulation that is as numerically and physically accurate as it is possible under the open-book schematization. The specification of the dynamic hydraulic diffusivity, replacing the kinematic hydraulic diffusivity, extends the diffusion wave model to the realm of dynamic waves (Ponce 1991). This assures the physical accuracy of the overland flow model through a wide range of Vedernikov numbers.
ONLINE OVERLAND uses the diffusion wave model
to calculate overland flow in an open-book schematization, using one book.
The appropriate specification of Courant number and
dynamic hydraulic diffusivity assures
a simulation that is as physically and numerically accurate as it is
possible in deterministic catchment modeling.
Thank you for running onlineoverland.php
[131022]
|