1. INTRODUCTION Throughout recorded history, human activities on the Earth's surface have been characterized by changes in land use and surface albedo. Typically, the changes have been from regions of lower albedo, e.g., dense forest or wetlands, to regions of higher albedo, such as rangelands, agricultural lands, and urban areas. The irrigation of arid lands, however, may have had the opposite effect (Stidd 1975; Anthes 1984; Budyko 1986). It is estimated that approximately 40% of the Earth's land surface is under the active management of humans, with more than 10% under cultivation (Eagleson 1986). The evidence linking increased surface albedo to decreased annual precipitation is mounting (Charney 1974; Balek 1983; Courel et al. 1984; Garrett 1993; Xue and Shukla 1993; Meehl 1994; Blyth et al. 1994). With the aid of global-scale models, these complex meteorological and hydroclimatological processes are now being better understood. Decreased precipitation leads to increased aridity and, therefore, to an increasing scarcity of environmental moisture, i.e., the moisture present in soil, land and air. The net result may have been a reduction in the supply of water resources, while the demand has continued to increase steadily (Eagleson 1986). While the mean planetary albedo is 0.34 (Houghton 1954), the mean albedo of the Earth's surface is only 0.15 (Otterman 1977). Actual values of ground surface albedo can range from as low as 0.07 for tropical rain forests to about 0.60 for hyperarid deserts (Sumner 1988). Moreover, higher values (0.75 - 0.95) are possible in the case of freshly fallen snow (Geiger 1965).
Since runoff is directly related to precipitation,
the water resources of the Earth are characterized by
the mean annual precipitation on a regional and local
basis. While global precipitation is around 1,030 mm,
the precipitation falling on peripheral continental
areas is 910 mm (L'vovich 1979).
The mean annual runoff coefficient.
i.e., the ratio of mean annual runoff to mean
annual precipitation, is also significantly
influenced by the climate (Budyko 1986).
Runoff coefficients range from near zero in
typical hyperarid regions to around 0.9 in
certain hyperhumid regions Over the years, the efforts of scientists in various disciplines have clarified the relationship between land use, surface albedo, and climate (Charney et al. 1975; Potter et al. 1975; Collins and Avissar 1994; Li and Avissar 1994; Glantz 1994). Here we extend Budyko's model (Budyko and Drozdov 1953b; Budyko 1986) of a coupled land surface-atmosphere system to assess changes in climate and water resources that may be linked to changes in land use and surface albedo. The objective is to develop a conceptual framework to evaluate the hydroclimatological impact of human activities. 2. ALBEDO AND LAND USE CHANGES
Albedo is the ratio of the total shortwave (0.3 - 3.0 mm)
radiation flux, reflected by a given surface in all directions,
to the total downwelling solar flux. The fraction of incoming
solar radiation absorbed and not reflected goes to: (1) warm
the earth's surface (sensible heat); (2) power the evaporation
process (latent heat); and (3) furnish the energy to sustain
various biochemical processes. Mean albedo is the average of reflectance factors in all spectral bands, weighted by the downwelling solar flux in each band (Irons et. al. 1988). Reflected radiance in each band is measured with a radiometer. These measurements can provide estimates within 3% accuracy (Ranson et. al. 1991). Alternatively, albedo can be measured by remote sensing, which offers the advantage of averaging albedo over large areas (Matthews and Rossow 1987; Gutman 1988). However, corrections need to be applied to remotely sensed albedo data to convert them to surface albedo (Koepke and Kriebel 1987; Gutman et. al. 1989). Table 1 shows typical values of mean albedo. These values range from as low as 0.03 (water surfaces with high solar elevation) to as high as 0.95 (freshly fallen snow). Several factors are shown to influence surface albedo, including: (1) time of day, i.e., the solar elevation or zenith angle; (2) season; (3) relief; (4) vegetative cover; (5) surface roughness and texture; (6) soil and rock type; (7) soil moisture; and (8) snow cover. Ostensibly, vegetative cover, surface roughness and texture, and soil moisture are subject to alteration by human action.
The albedo of bare soil is affected not only by its
texture and color, but also by its water content. Changes in land use have the potential to change albedo. Water and vegetation surfaces have lower albedos than do dry, bare soil surfaces. Soil moisture is the crucial parameter in the land use-albedo relation, since albedo increases markedly with a decrease in soil moisture. Forests have typically lower albedos than do rangelands; in turn, rangelands have lower albedos than does dry bare ground. The evidence regarding the effect of agricultural land use on albedo is mixed. Albedos of most crops are higher than those of forests, but comparable to those of rangelands. Likewise, the effect of urbanization on albedo is mixed. Some cities will produce marked increases in albedo, while others, particularly those featuring an abundance of green areas, may not. Otterman (1977) has stated that the Earth's means surface albedo might presently be 0.154, whereas about 6,000 years ago it might have been only 0.14. He attributes this 10% increase to the effect of humans and other grazing species. This estimate is to be taken as a global average. Considering that some remote regions have been subject to very little alteration, marked increases in albedo may have already occurred in some heavily disturbed, altered, or developed areas. Deforestation, overgrazing, overcultivation, and ground-water depletion may be responsible for albedo increases. 3. ALBEDO AND CLIMATIC CHANGES Precipitation occurs when the following conditions are met (U.S. 1970; Branson et. al. 1981):
The simultaneous occurrence of several of the previously
mentioned processes is usually necessary for heavy
precipitation to occur. Of all the mechanisms that
contribute to precipitation, thermal lifting stands
out as one that is readily subject to a large-scale
modification by human activities.
Charney (1974) pioneered the study of the relationship
between albedo and climate. He reasoned that a decrease
in plant cover is usually accompanied by an increase in
albedo. This leads to a decrease in absorbed radiation,
which leads to an increase in the radiative cooling of
the air (since land surface warming is critical to the
radiative warming of the planetary boundary layer). Further research has shown that the mechanism by which an increase in surface albedo led to cooling of the near-ground air and a consequent decrease in rainfall is somewhat more complicated than the original Charney model, which is applicable to a desert with no evaporation. While the increase in surface albedo reduced the absorption of solar radiation by the ground, it also reduced the transfer of sensible and latent heat from the ground to the atmosphere. This increase in surface albedo caused a decrease in cloud amount and precipitation, which decreased the planetary albedo. In most cases, the reduction of cloud amount was so great that the decrease in planetary albedo counteracted the increase in surface albedo and caused a net increase in the absorption of solar radiation at the ground. However, due to the reduction in cloudiness, there was an even greater increase in the net loss of longwave radiation from the ground, since the downward longwave radiation from a cloud is much greater than that of a cloudless atmosphere. The result was that the increase in surface albedo resulted in a decrease in the net absorption of solar plus long-wave radiation (Charney et. al. 1977). Using a general circulation model (GCM), Sud and Molod (1988) have concluded that for arid and semiarid regions, the overall effect of high surface albedo is that of cooling inside the planetary boundary layer. This cooling induces sinking aloft and moisture divergence near the surface, both of which suppress moisture convection and rainfall. Thus, in a desert border region, an increase in surface albedo would be expected to reduce the convective rainfall locally.
The link between albedo and precipitation has been
documented in GCM studies conducted over the past two
decades. Charney et at. (1975) showed that July
precipitation over the Sahara was Blyth et. al. (1994) used a GCM to show that forests can have a considerable effect on rainfall in a frontal situation. The total rainfall, when the surface was covered by forest, was 30% higher than when the surface was all bare soil. Mylne and Rowntree (1991) reported results for regions within 20° of the equator. They focused on the impact of tropical deforestation on surface albedo and climatic changes. Their results suggest a 20% decrease in regional rainfall for a 0.1 increase in albedo, with more than half of this decrease being the result of changed moisture convergence.
Meehl (1994) studied the relationship between
surface albedo and soil moisture in accounting
for the reduced precipitation in general
circulation modeling of the Asian summer monsoon.
Garratt (1993) has recently surmmarized the response of global climate simulations to changes in albedo. The results of eleven (11) studies showed that increases in albedo cause: (1) decreased land evaporation; (2) decreased land precipitation; and (3) increased precipitation over the sea, in the global change cases. These and other related studies support the statement that increased surface albedo leads to local/regional climatic changes in the direction of greater aridity. 4. BUDYKO'S HYDROCLIMATOLOGICAL MODEL
A basin's mean annual runoff coefficient characterizes the supply of
surface water. In endorheic (interior, or closed) drainages, the
runoff coefficient is zero. Conversely, in exorheic (exterior, or open)
drainages, the runoff coefficient generally increases with environmental
moisture, across the climatic spectrum, from hyperarid to hyperhumid
regions (L'vovich 1979; Budyko 1986). The annual water balance for an exorheic drainage basin is expressed as follows:
where P = precipitation; E = evaporation; Q = total runoff (consisting of surface runoff, Qs and ground-water runoff, Qg); and ∆S = change in basin storage. The basin storage consists of surface, subsurface, and ground-water storage. In an average year, Eq. 1 reduces to the following:
where, unlike in Eq. 1, the values in Eq. 2 are taken as mean annual values. Equation 2 assumes that deep percolation, i.e., the ground-water runoff that discharges directly into the sea, bypassing the surface waters, is negligible. We note that on a global basis, L'vovich (1979) has calculated that deep percolation is approximately 5% of runoff, while the latter is approximately 30% of precipitation. Thus, in general, only a small fraction of precipitation (less than 2%) infiltrates deep enough into the ground to bypass the surface waters.
The separation of annual precipitation from a hydroclimatological perspective
was pioneered by Budyko and Drozdov (1953b) (World 1978).
The basic elements of the model are described here.
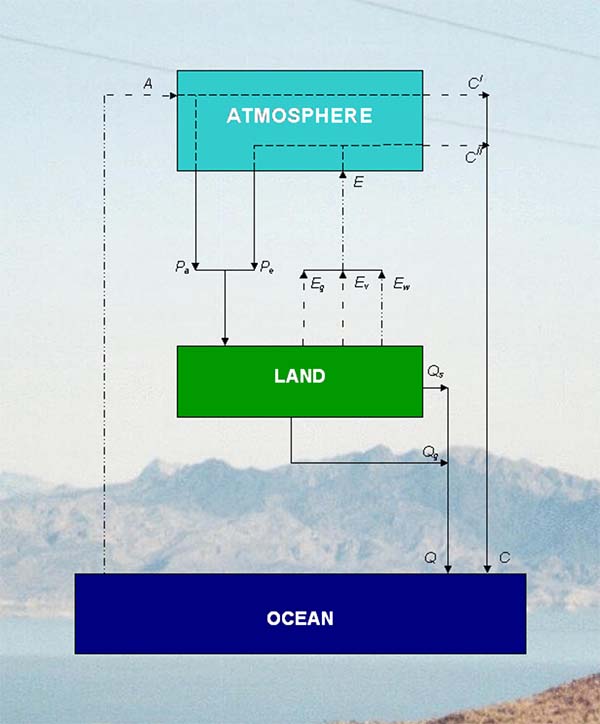
Let A be the water vapor entering the control volume
through horizontal advection, i.e., the input advected water
vapor; and E be the amount of land-surface evaporation,
i.e., the water vapor entering the control volume vertically,
through evaporation from the land (the combined evaporation
from soil, land surface, and vegetation) (Fig. 1). Therefore:
in which P = annual precipitation; Pa = fraction of P derived externally, from A; and Pe = fraction of P derived internally from E.
From Fig. 1, conservation of mass leads to:
where C = total water vapor measured at leeward side of control volume (i.e., output water vapor). Furthermore
where C' = water vapor in transit; i.e., fraction of advected water vapor that does not precipitate within control volume and exits at leeward side, defined as follows:
subject to C' ≥ 0; and C" = water vapor discharge; i.e., fraction of evaporated water vapor that does not recycle and, instead, leaves the control volume at the leeward side, defined as follows:
subject to C" ≥ 0.
In formulating his model, Budyko assumed that P and E
are spatially averaged within the control volume. The external (advected)
water vapor flux at the windward side of the control volume is
WU, W is the moisture content of the atmospheric column
and U is the mean velocity of the input advected water vapor.
Assuming a linear decrease in advected water vapor flux as the moist
air moves across the region, the corresponding flux at the leeward side
is WU - PaL, where L is a lengthscale
measure of the control volume (taken as the square root of the area of
its vertical projection). Thus, the external water vapor flux, spatially
averaged over the control volume, is The internal (i.e., evaporated) water vapor flux at the windward side of the control volume is zero; the corresponding flux at the leeward side, assuming a linear decrease as the moist air moves across the region, is (E - Pe)L. Thus, the internal water vapor flux, spatially averaged over the control volume, is (1/2)(E - Pe)L.
The atmosphere is assumed to be completely mixed, so
that the ratio of externally to internally derived
precipitation Pa/Pe
is equal to the ratio of spatially averaged external
to internal water vapor fluxes. This leads to
in which Ω = dimensionless climatic parameter (Entekhabi et al. 1992) defined as
The quantity Ω-1 has been referred by Eagleson (1994) as the Budyko parameter. Using Eq. 3 and Eq. 8, annual precipitation can be separated into
and
Budyko defined a moisture cycling coefficient k
= P/Pa = 1 + Ω, interpreted
as the number of cycles completed by the local water vapor
before it is eventually removed from the control volume.
Values of Ω ranging from 0.02 (Antarctica: inner continental region), to 0.05 (Australia: Pacific Ocean drainages), to 0.34 (North America: Atlantic Ocean drainages), to 0.68 (South America: whole continent) have been documented in World (1978). Low values of Ω (0.02 - 0.10) indicate a hyperarid/arid climate; average values (0.15 - 0.30) indicate a semiarid/subhumid climate; high values (0.50 - 0.70) indicate a humid/hyperhumid climate.
For instance, in an arid region,
with P = 250 mm yr-1; E =
240 mm yr-1, L = 500 km, W =
20 mm, and U = 200 km d-1. Then,
Ω = 0.04, k = 1.04, Pa = 240
mm yr-1, and Pe = 10
mm yr-1. In this case, since Pe
is small compared to Pa, most of the
precipitation originates in the advection of external
water vapor, and only a small fraction of it is traceable
to moisture recycling. As another example, in a subhumid
region, with P = 1,500 mm yr-1;
E = 1,100 mm yr-1, L =
1,000 km, W = 50 mm, and The evaporation originates from three distinct sources (Fig. 1)
where Eg = evaporation from bare ground; Ev = evaporation from vegetated surfaces, i.e., evapotranspiration; and Ew = evaporation from water bodies. The fate of evaporation is either to recycle as Pe or to exit the control volume as water vapor discharge C'' (Fig. 1). Equations 10 and 11 were derived assuming a linear decrease in water vapor fluxes as the moist air is transposed across the control volume. This limits the applicability of these equations to regions with L ≤ 1,500 km. For larger regions, the relaxation of the linearity assumption leads to somewhat more elaborate formulas (World 1978; Brubaker et. al. 1993). From Eqs. 10 and 11, it is seen that Pe /P increases with Ω. The higher the evaporative flux (EL/2) compared to the advective flux (WU), the higher the Ω and the higher the Pe implying that a greater fraction of evaporation is being recycled. Conversely, the lower the evaporative flux compared to the advective flux, the lower the Ω and the lower the Pe , implying that a greater fraction of evaporation is leaving the control volume as water vapor discharge. 5. RELATIONSHIP WITH SURFACE ALBEDO The lower albedos associated with open water, vegetation, and moist land surfaces make possible the increased absorption of solar and longwave radiation, resulting in increased evaporation and increased environmental moisture. It follows that albedo is intrinsically related to environmental moisture. In turn, environmental moisture is directly related to the climatic parameter Ω and, therefore, to the moisture recycling capacity of the coupled land surface-atmosphere system.
From a somewhat different perspective, increased
environmental moisture implies that the source of
most of the evaporation is Ev +
Ew (typical of a humid region).
Conversely, decreased environmental moisture implies
that the source of most of the evaporation is
Eg (typical of an arid region).
Several studies have documented the relationship between environmental moisture and the recycling capacity of the coupled land surface-atmosphere system. Benton et. al. (1950) estimated that the portion of precipitation derived from local evapotranspiration for the Mississippi valley was at most 10%. The same percentage was estimated by Budyko and Drozdov (1953a) for the European portion of the former USSR. In the humid Amazon basin, Salati et. al. (1979) and Salati and Vose (1984) have measured a recycling rate of 48%, while Lettau et. al. (1979) have found that 88.4% of the total amount of rain at 75°W longitude in the Amazon basin falls at least a second time. In some instances, anthropogenic effects on the moisture recycling capacity may be substantial. For instance, Stidd (1975) has reported that evapotranspiration from irrigation development in the Columbia basin was recycled at least once as rainfall. Moreover, Balek (1983) has stated that an increase in annual rainfall of 5% to 10% in the vicinity of Kariba dam, in Africa, was traceable to increased evaporation after the establishment of the lake. 6. WATER BALANCE COEFFICIENTS To extend Budyko's model to assess the potential hydroclimatological impact of human activities, we define the following set of water balance coefficients: Moisture recycling coefficient Kc
Water vapor discharge coefficient Kd
Runoff coefficient
Conservation of mass requires that:
Equations 13-16 are used to analyze the variation of water balance coefficients across the climatic spectrum, from hyperarid (P = 125 mm yr-1) to hyperhumid (P = 4,000 mm yr-1) climates. Table 2 shows a typical calculation for six climatic types (column 1). Values of albedo α (column 2) were esti-mated based on the literature (Eagleson 1970; Lee 1980; Sumner 1988) and are shown here for reference purposes only. Values of Ω (column 3) were estimated based on World (1978), as a function of climatic type. Values of mean annual precipitation P (column 4) were based on
To estimate the input advected water vapor A, the average moisture present in the atmospheric column for the subhumid
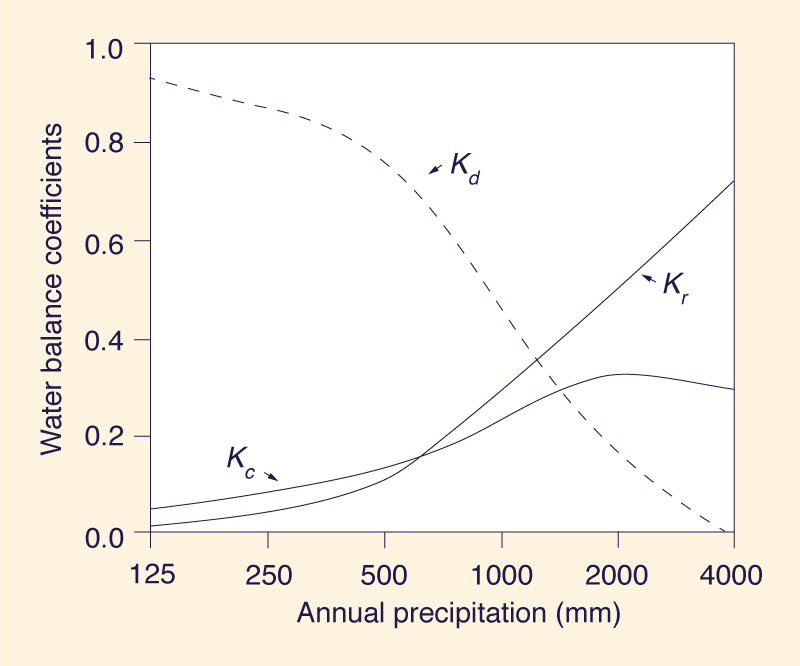
climatic type was assumed to be 30 mm, and the recycling period of atmospheric moisture 11 d. Therefore, A = (30 mm cycle-1) x (365 d yr-1)/(11 d cycle-1) = Water vapor in transit C' (column 10) was calculated using Eq. 6. Water vapor discharge C'' (column 11) was calculated using Eq. 7. The output advected water vapor C (column 12) was calculated using Eq. 5. Eq. 4 was confirmed for all cases; i.e., the sum of runoff Q plus output water vapor C is equal to the input advected water vapor A. The moisture recycling coefficient Kc (column 13) was calculated using Eq. 13. The water vapor discharge coefficient Kd (column 14) was calculated using Eq. 14. Eq. 16 (mass conservation) was confirmed in all cases. The calculations shown in Table 2 are subject to the constraint C'' ≥ 0; that is, the fraction of precipitation derived internally ( Pe ) cannot exceed the amount of evaporation ( E ). This constraint is in effect for high values of Ω, specifically when Ω > E/Q (for example, the hyperhumid one of Table 2). It can be shown that at the limit, when Ω = E/Q, then Q = Pa , i.e., the entire fraction of precipitation derived externally ( Pa ) will constitute runoff ( Q ), with none of it going to water vapor discharge ( C" ). In the hyperhumid case shown in Table 2, if the physical constraint Pe ≤ E had not been enforced, the values of Pa, Pe, C', and C'' calculated using Eq. 10, Eq. 11, Eq. 6, and Eq. 7 would have been 2,353, 1,647, 647, and -447 mm, respectively. However, since C" ≥ 0, the water vapor discharge (-447 mm) is algebraically added to the calculated value of Pe to give a corrected value Pe = 1,200 mm, and is subtracted from the calculated value of Pa to give a corrected value Pa = 2,800 mm. Thus, the corrected values C' = 200 mm and C'' = 0 are calculated. This deviation from Budyko's partitioning of precipitation for sufficiently high values of Ω is necessary to satisfy mass conservation and avoid negative values of Kd. In other words, the high values of Kr typical of some hyperhumid regions are possible only at the expense of correspondingly low values of Kc and lower values of Kd. The results of Table 2 are plotted in Fig. 2. The following observations are noted:
Shown in column 2 of Table 2 are typical values of albedo ( α ) for each climatic type, wherein albedo is inversely related to Ω. As albedo increases, Ω decreases, which in turn increases water vapor discharge and decreases moisture recycling and runoff. Conversely, a decrease in albedo decreases water vapor discharge and increases moisture recycling and runoff.
7. HYDROCLIMATOLOGICAL IMPACT OF HUMAN ACTIVITIES The relationship between water balance coefficients and annual precipitation shown in Fig. 2 has significant implications for assessing the hydroclimatological impact of human activities. While the runoff coefficient Kr and the water vapor discharge coefficient Kd increase and decrease monotonically, respectively with annual precipitation, the moisture recycling coefficient Kc shows a definite peak at P ≈ 2,000 mm. This implies that in regions with P ≥ 2,000 mm, changes in albedo (through deforestation, overgrazing, overcultivation, and other related land surface disturbances) result in slight changes in Kc. Conversely, in regions with P < 2,000 mm, increases in albedo result in substantial decreases in Kc and Kr, and consequent increases in Kd. This confirms the observation that changes in albedo are of particular significance along the middle-to-dry side of the climatic spectrum (dry subhumid to semiarid), where the hydroclimatological response to albedo modification is likely to be more marked. 8. SUMMARY AND CONCLUSIONS The relation between land use, surface albedo, climate, and water resources is examined by extending Budyko's hydroclimatological model (Budyko 1986) to the calculation of water balance coefficients across the climate spectrum. Land use changes attributable to anthropogenic activities have often led to increases in albedo. Surface albedo is shown to be closely connected with the prevailing climate. Increases in surface albedo cause decreases in precipitation following a phenomenological model postulated by Charney (1974) and Charney et. al. (1977). The water vapor discharge and the moisture recycling capacity of the coupled land surface-atmosphere system are related to the climatic parameter Ω. In turn, Ω is inversely related to surface albedo. A set of water balance coefficients is developed to characterize hydroclimatological phenomena across the climatic spectrum. These are the following: (1) moisture recycling coefficient kc; (2) water vapor discharge coefficient kd; and (3) runoff coefficient kr. Mass conservation requires that the sum of the three coefficients be equal to one. In hyperarid regions, atmospheric moisture goes almost entirely to water vapor discharge, with moisture recycling and runoff being reduced to a minimum. Conversely, in humid and hyperhumid regions, moisture is more or less evenly divided between recycling and runoff, with water vapor discharge reduced to a minimum. Moreover, at the middle of the climatic spectrum (dry subhumid), all three water balance coefficients have comparable values. ACKNOWLEDGMENTS Anil K. Lohani spent four months on assignment at San Diego State University, on leave from the Ganga Plains Regional Centre, National Institute of Hydrology, Patna, Bihar, India. His leave was funded by the United Nations Development Programme. APPENDIX I. REFERENCES
Anthes, R. A. 1984. "Enhancement of convective precipitation by mesoscale variations in vegetative covering in semiarid regions." J. Climate and Appl. Meteorology, 23, 541-554.
Balek, J. 1983. "Hydrology and water resources in tropical regions." Developments in water science, 18, Elsevier Science Publishers BV, Amsterdam, The Netherlands.
Beaton, G. S., R. T. Blackburn, and V. O. Snead. 1950. "The role of the atmosphere in the hydrologic cycle." Eos Trans., AGU, 31(1) 61-73.
Blyth, E.M., A. J. Dolman, and J. Noilhan. 1994. "The effect of forest on mesoscale rainfall: an example from HAPEX-MOBILHY." J. Appl. Meteorology, 33, 445-454.
Branson, F. A., G. F., Gifford, K. G.
Renard, and R. F. Hadley. 1981. Rangeland hydrology, 2nd Ed. Range Sci. no. 1, Soc. for Range Mgmt., Denver, Colo.
Brubaker, K. L., D. Entekhabi, and P S. Eagleson. 1993. "Estimation of continental precipitation recycling." J. Climate, 6, 1077-1089.
Budyko,M.I. 1986. The evolution of the biosphere. D. Reidel Publishing Co., Boston.
Budyko,M. I., and O. A. Drozdov. 1953a. "Characteristics of the moisture circulation in the atmosphere." Izv. Akad.Nauk.SSSR Ser. Geogr. Geofiz., 4, 5-14.
Budyko, M.I., and O. A. Drozdov. 1953b. "The laws of water cycle in the amosphere." Bull. Acad. Sci. USSR, Ser.: Georg., 4, 167-170.
Charney, J. 1974. Paper Presented at Symons Lect., Q. J. R. Meteorological Soc., Royal Meteorological Soc., London.
Charney, J., W. J. Quirk, S-H. Chow, and J. Kornfeld, J. 1977. "A comparative study of the effects of albedo change on drought conditions in semiarid regions." J. Atmospheric Sci., 36, 1366-1385.
Charney. J., P. H. Stone, and W. J. Quirk. 1975. "Drought in the Sahara: biophysical feedback mechanism." Science, 187, 434-435.
Collins, D. C., and R. Avissar. 1994. "An evaluation with the Fourier Amplitude Sensitivity Test (PAST) of which land-surface parameters are of greatest importance in atmospheric modeling." J. Climate, 7, 681-703.
Comisión del Papaloapan. 1975. Atlas climatologico e hidrológico de la Cuenca del Papaloapan (Climatological and hydrological atlas of the Papaloapan River Basin). Ingeniería y Procesamiento Electrónico, Mexico, D.F., Mexico.
Courel. M. F., R. S. Kandel, and S. I. Rasool. 1984. "Surface albedo and the Sahel drought" Nature, 307. 528-531.
Dickinson, R. E. 1983. "Land surface processes and climate-surface albedos and energy balance." Adv. in Geophys., 25, 305-353.
Eagleson, P.S. 1970. Dynamic hydrology. McGraw-Hill Book Co., Inc., New York, N.Y.
Eagleson, P. S. 1986. "The emergence of global-scale hydrology." Water Resour. Res., 22, 6S-14s.
Eagleson. P. S. (1994). "The evolution of modern hydrology (from watershed to continent in 30 years)." Adv. in Water Resour., 17, 3-18.
Entekhabi,D., I. Rodriguez-lturbe, and R. L. Bras. 1992. "Variability in large-scale water balance with land surface-atmosphere interaction." J. Climate, 5, 798-813.
Garratt. J. R. 1993. "Sensitivity of climate simulations to land-surface and atmospheric boundary-layer treatments. - a review." J.Climate, 6, 419-449.
Geiger, R. 1965. The climate near the ground. Harvard Univ. Press, Cambridge, Mass. (in German).
Glantz, M. H. 1994. Drought follows the plow: cultivating marginal areas. Cambridge University Press, London.
Gutman, G. 1988. "A simple method for estimating monthly mean albedo of land surfaces from AVHRR data." J. Appl. Meteorology, 27, 973-988
Gutman, G., G. Ohring, D. Tarpley, and R. Ambroziak. 1989, "Albedo of the U.S. Great Plains as determined from NOAA-9 AVHRR data" J. Climate, 2, 608-617.
Ioughton. H. G. 1954. "On the annual heat balance of the northern hemisphere." J.Meteorology, 11(1), 1 - 9.
Irons, J. R., K. J. Ranson, and C. S. T. Daughtry, 1988. "Estimating big bluestern albedo from directional reflectance measurements." Remote Sens. Envir., 25, 185-199.
Koepke, P., and K. T. Kriebel. 1987. "Improvements in the shortwave cloud-free radiation budget accuracy, part I: numerical study including surface anisotropy." J. Climate and Appl. Meteorology, 26, 374-395.
Lee, R. 1980. Forest hydrology. Columbia University Press, New York, N.Y.
Lettau, H., K. Lettau, and L. C. B. Molion. 1979. "Amazonia's hydrologic cycle and the role of atmospheric recycling in assessing deforestation effects." Monthly Weather Rev., 107, 227-237.
Li. B., and R. Avissar. 1994. "The impact of spatial variability of landsurface characteristics on land-surface heat fluxes." J. Climate, 7, 527-537.
L'vovich, M. I. 1979. World water resources and their future. American Geophysical Union, Washington, D.C. (in Russian).
Matthews, E., and W. B. Rossow. 1987. "Regional and seasonal variations of surface reflectance from satellite observations at 0.6 mm." J. Climate and Appl. Meteorology, 26, 170-202.
McNaughton, K. G., and P. G. Jarvis. 1983. "Predicting effects of vegetation changes on transpiration and evaporation." Water deficits and plant growth, T.T. Kozlowski,ed., Academic Press, New York, N.Y., 1-47.
Meehl, G. A. 1994. "Influence of the land surface in the Asian summer monsoon: external conditions versus internal feedback." J. Climate, 7, 1033-1049.
Myers, V. I., and W. A. Allan. 1968.. "Electrooptical remore sensing methods as nondestructive testing and measuring techniques in agriculture." Appl. Optics, 7(9), 1819-1838.
Mylne, M. F., and P. R. Rowntree. 1991. "Deforestation of Amazonia: modeling the effects of albedo change." Clim. Res. Tech. Note CRTN 7, Hadley Ctr., U.K. Met. Ofc., Bracknell.
Oke, T. R. 1978. Boundary layer climates, 2nd Ed., Methuen, London.
Otterman, J. 1977. "Anthropogenic impact on the albedo of the Earth." Climatic Change, 1, 137-155.
Ponce, V. M. 1995. "Management of droughts and floods in the semiarid Brazilian Northeast-the case for conservation." J. Soil Water Conservation, 50(5), 422-431.
Porter, A. 1969. Cybernetics simplffled. The English Universities Press Ltd., London.
Potter, G. L., H. W. Ellsaesser, M. C.
McCracken, and F. M. Luther. 1975. "Possible climatic impact of tropical deforestation." Nature, 258(5,537), 697-699.
Ranson K. J., J. R. Irons, and C. S. T. Daughtry. 1991. "Surface albedo from bidirectional reflectance." Remote Sens. Envir., 35, 201-211.
Salati, E., A. Dall'Olio, E. Matsui, and J. R. Gat. 1979. "Recycling of water in the Amazon basin: an isotopic study." Water Resour. Res., 15(5), 1250-1258.
Salati, E., and P. B. Vose. 1984. "Amazon basin: a system in equilibrium." Science, 225(4,658), 129-138.
Stidd, C. K. 1975. "Irrigation increases rainfall?" Science, 188, 279-280.
Sud, Y. C., and A. Molod. 1988. "A GCM simulation study of the influence of Saharan evapotranspiration and surface-albedo anomalies on July circulation and rainfall." Monthly Weather Rev., 116, 2388-2400.
Sumner, G. 1988. Precipitation: processes and analysis. J. Wiley & Sons, Inc., New York, N. Y.
Tricart, J. 1982. "El Pantanal: un ejemplo del impacto de la geomorfología sobre el medio ambiente (The Pantanal: an example of the impact of geomorphology on the environment)." Geografía, Sao Paulo, Brazil, 7(13-14), 37-50.
U.S. Dept. of Agriculture. 1970. "Fire weather." Agriculture Handbook 360. USDA Forest Service.
World water balance and water resources of the Earth. 1978. USSR Com. for the Int. Hydro. Decade, UNESCO, Paris (in Russian).
Xue, Y., and J. Shukla. 1993. "The influence of land surface properties on Sahel climate-part I: desertification." J. Climate, 6, 2232-2245.
APPENDIX II. NOTATION
The following symbols ars used in this paper:
A = input advected water vapor;
C = output water vapor, (5);
C' = water vapor in transit, (6);
C'' = ware vapor discharge, (7);
E = annual evaporation;
Eg = evaporation from bare ground;
Ev = evaporation from vegetated surfaces;
Ew = evaporation from water bodies;
Kc = moisture recycling coefficient, (13);
Kd = Water vapor discharge coefficient, (14);
Kr = runoff coefficient, (15);
K = Budyko's moisture cycling coefficient;
L = length-scale measure of control volume;
P = annual precipitation;
Pa = fraction of precipitation derived from advected water vapor, (10);
Pe = fraction of precipitation derived from evaporation (11);
Q = total annual runoff;
Qs = surface runoff;
Qg = ground-water runoff;
U = mean velocity of input advected water vapor;
W = moisture content of atmospheric column;
α = albedo;
∆S = change in basin storage; and
Ω = dimensionless climatic parameter (9).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 220925 |
| Documents in Portable Document Format (PDF) require Adobe Acrobat Reader 5.0 or higher to view; download Adobe Acrobat Reader. |